Anche in architettura i numeri sono fondamentali, perchè rappresentano la misura e le relazioni che intercorrono tra le parti. La simmetria, appunto, rappresenta la corrispondenza tra ciascuna parte presa singolarmente e l’insieme. Si fa strada con questo concetto il significato di modulo: la simmetria infatti si realizza attraverso base modulare. Proprio in riferimento a ciò, Vitruvio fu forse l'unico a ipotizzare la possibilità di scomporre un corpo in varie parti (o moduli) a loro volta scomponibili in sottoparti, tutte rappresentate da numeri interi: la commodulatio. Inoltre, sottolinea l'importanza delle proporzioni del corpo umano, in quanto afferma che è impossibile proporzionare un tempio senza far riferimento ad esse.
Il proporzionamento statico, quindi, non è altro che l'utilizzo di rapporti di numeri interi in strutture metriche commensurabili, cioè di due o più grandezze omogenee che implichino un sottomultiplo comune.
es: 24/16 ha un'unità comune, 4 o il suo multiplo 8. Quindi un rettangolo 24x16cm conterrà al suo interno:


4 rettangoli 12x8cm 16 rettangoli 8x4cm 64 rettangoli 4x1cm
Quindi, nel momento in cui ci ritroveremo ad analizzare il proporzionamento statico di un edificio, significa che staremo trovando quel modulo, quella forma geometrica che, ripetuta per un tot numero di volte, ci da la forma e la misura complessiva dell'edificio o di parte di esso.
SEZIONE AUREA
Molti di voi probabilmente non conoscono queste due parole, ma vi assicuro che vi sono capitate davanti agli occhi un milione di volte. Dove? Quando? Ogni volta che in un campo di girasoli avete ammirato questo bellissimo fiore, o raccolto una conchiglia di alcuni molluschi, o ancora osservando le foto di alcune galassie: la sezione aurea si nasconde in ogni fenomeno naturale.
Questo rapporto si basa sul numero aureo, un numero irrazionale poco maggiore di 1 (1,6180339887..), composto da infinite cifre, a differenza del numero scaturito dai rapporti del proporzionamento statico che è finito. Proprio per questo la sezione aurea ed il rettangolo radical (che vedremo più avanti) sono proporzionamenti dinamici.
Il numero aureo, indicato con la lettera Phi (φ), fu scoperto dagli antichi greci ma fu Euclide a tramandarlo nel tempo attraverso il suo libro Elementi di Geometria, scritto intorno al 300 a.C.
In realtà la denominazione φ fu data solo all'inizio del XX secolo, quando il matematico nordamericano Mark Barr legò il numero a Fidia, l'architetto che progettò il Partenone di Atene.
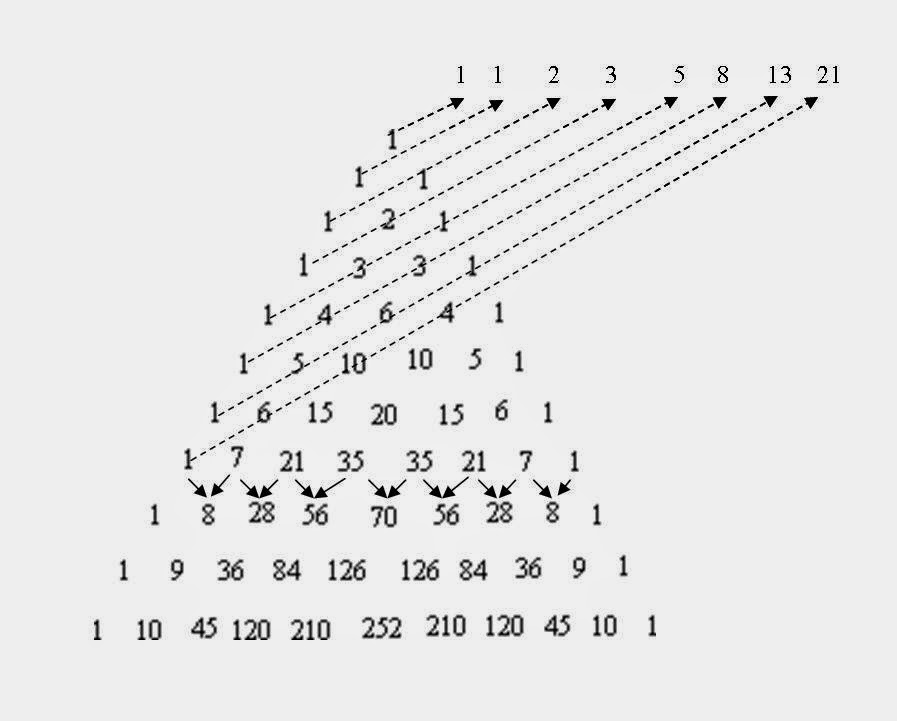
E' interessante notare che il numero aureo ha relazione anche con la Serie di Fibonacci o con L'uomo vitruviano di Leonardo: con la prima perchè Fibonacci, matematico italiano del XIII secolo, descrisse una serie che inizia con i valori 1 e 1, a partire dai quali ogni nuovo termine viene generato dalla somma dei due precedenti. Il quoziente di un numero qualsiasi della successione ed il suo precedente si approssima a φ sempre più man mano che si procede con la serie; infatti, arrivati al quarantesimo termine il quoziente si approssima con una precisione di 14 decimali.
Euclide, a suo tempo, chiama φ in un altro modo, ossia media ed estrema ragione: un segmento è diviso in media ed estrema ragione quando l’intero segmento sta alla sua parte maggiore, come quest’ultima sta alla minore.
2) Puntiamo il compasso in C, con apertura CB, e disegniamo l'arco che interseca
l'ipotenusa AC nel punto X.
3) Puntiamo il compasso in A, con apertura AX, e disegniamo l'arco che interseca
il cateto AB nel punto Y.
AY è la sezione aurea, in quanto AB:AY=AY:AB=φ
È interessante notare inoltre che la sezione aurea riproduce infinitamente se stessa: se si riporta un segmento uguale al segmento minore sulla parte maggiore, quest'ultima risulta evidentemente divisa di nuovo in media ed estrema ragione. Stessa cosa accade per i rettangoli aurei.
COSTRUZIONE DI UN RETTANGOLO AUREO
1) Disegniamo il quadrato ABCD e troviamo il punto medio M del lato AB.
2) Puntiamo in M, con apertura MC, e tracciamo un arco di circonferenza che andrà ad intersecarsi con il prolungamento del lato AB nel punto E.
AEFG è il rettangolo aureo.
COSTRUZIONE DI UN RETTANGOLO
1) Disegniamo il quadrato ABCD.
2) Puntiamo in A, con apertura AC, e tracciamo un arco di circonferenza che andrà ad intersecarsi con il prolungamento del lato AB nel punto E.
AEFG è il rettangolo aureo.
Si può continuare all'infinito, trovando ulteriori rettangoli radical, basta mandare un'altra diagonale AF e ripetere la procedura.
Partenope
Il numero aureo, indicato con la lettera Phi (φ), fu scoperto dagli antichi greci ma fu Euclide a tramandarlo nel tempo attraverso il suo libro Elementi di Geometria, scritto intorno al 300 a.C.
In realtà la denominazione φ fu data solo all'inizio del XX secolo, quando il matematico nordamericano Mark Barr legò il numero a Fidia, l'architetto che progettò il Partenone di Atene.
E' interessante notare che il numero aureo ha relazione anche con la Serie di Fibonacci o con L'uomo vitruviano di Leonardo: con la prima perchè Fibonacci, matematico italiano del XIII secolo, descrisse una serie che inizia con i valori 1 e 1, a partire dai quali ogni nuovo termine viene generato dalla somma dei due precedenti. Il quoziente di un numero qualsiasi della successione ed il suo precedente si approssima a φ sempre più man mano che si procede con la serie; infatti, arrivati al quarantesimo termine il quoziente si approssima con una precisione di 14 decimali.
Con Leonardo perchè L'uomo ideale o Vitruviano mostra le proporzioni del ideali del corpo umano mettendolo in relazione con la geometria e iscrivendolo in un quadrato e un cerchio. La ragione tra il lato del quadrato e il raggio del cerchio è aurea.
Euclide, a suo tempo, chiama φ in un altro modo, ossia media ed estrema ragione: un segmento è diviso in media ed estrema ragione quando l’intero segmento sta alla sua parte maggiore, come quest’ultima sta alla minore.
In poche parole, significa dividere un segmento in due parti diseguali, tali che la maggiore abbia con la minore lo stesso quoziente (φ) che l'intero segmento ha
con la parte maggiore.
Ecco come si divide un segmento in media ed estrema ragione:
1) Costruiamo un triangolo rettangolo con cateti AB e AB/22) Puntiamo il compasso in C, con apertura CB, e disegniamo l'arco che interseca
l'ipotenusa AC nel punto X.
3) Puntiamo il compasso in A, con apertura AX, e disegniamo l'arco che interseca
il cateto AB nel punto Y.
AY è la sezione aurea, in quanto AB:AY=AY:AB=φ
È interessante notare inoltre che la sezione aurea riproduce infinitamente se stessa: se si riporta un segmento uguale al segmento minore sulla parte maggiore, quest'ultima risulta evidentemente divisa di nuovo in media ed estrema ragione. Stessa cosa accade per i rettangoli aurei.
COSTRUZIONE DI UN RETTANGOLO AUREO
1) Disegniamo il quadrato ABCD e troviamo il punto medio M del lato AB.
2) Puntiamo in M, con apertura MC, e tracciamo un arco di circonferenza che andrà ad intersecarsi con il prolungamento del lato AB nel punto E.
AEFG è il rettangolo aureo.
COSTRUZIONE DI UN RETTANGOLO
2) Puntiamo in A, con apertura AC, e tracciamo un arco di circonferenza che andrà ad intersecarsi con il prolungamento del lato AB nel punto E.
AEFG è il rettangolo aureo.
Si può continuare all'infinito, trovando ulteriori rettangoli radical, basta mandare un'altra diagonale AF e ripetere la procedura.
Se dividiamo il lato maggiore per la metà otterremo un Rettangolo Radical dimezzato rispetto a quello iniziale.
Partenope








-hq-front.jpg)

.jpg)

Nessun commento:
Posta un commento